 .
.Dies sind die Ergebnisse des 3. OWINF vom 23.09.2006. Wir gratulieren allen Teilnehmern ganz herzlich zu Ihrem Erfolg.
| Name | handy | klammerwald | theater | ∑ |
|---|---|---|---|---|
| Dominik Reichl |
85
|
50
|
100
|
235 |
| N.N. |
x
|
100
|
100
|
200 |
| Martin Maas |
50
|
50
|
90
|
190 |
| Daniel Grunwald |
50
|
50
|
85
|
185 |
| Benito van der Zander |
100
|
35
|
30
|
165 |
| N.N. |
50
|
45
|
70
|
165 |
| Arne Müller |
30
|
50
|
60
|
140 |
| Mathis Block |
x
|
50
|
80
|
130 |
| Fabian Gundlach |
25
|
x
|
100
|
125 |
| Marvin Künnemann |
25
|
x
|
100
|
125 |
| Urs Hanselmann |
25
|
x
|
100
|
125 |
| Andreas Krüger |
x
|
50
|
70
|
120 |
| Birtan Özel |
50
|
0
|
60
|
110 |
| Julian Fischer |
20
|
50
|
40
|
110 |
| Sören Jentzsch |
0
|
x
|
100
|
100 |
| Christian Koch |
x
|
0
|
100
|
100 |
| N.N. |
x
|
x
|
100
|
100 |
| Thi Bui-Ngoc |
x
|
0
|
100
|
100 |
| N.N. |
25
|
x
|
60
|
85 |
| N.N. |
x
|
30
|
50
|
80 |
| N.N. |
x
|
0
|
70
|
70 |
| N.N. |
x
|
0
|
70
|
70 |
| N.N. |
25
|
0
|
40
|
65 |
| N.N. |
40
|
0
|
20
|
60 |
| N.N. |
45
|
x
|
10
|
55 |
| N.N. |
x
|
45
|
10
|
55 |
| N.N. |
x
|
50
|
x
|
50 |
| N.N. |
x
|
x
|
50
|
50 |
| N.N. |
x
|
x
|
50
|
50 |
| N.N. |
x
|
x
|
30
|
30 |
| N.N. |
5
|
x
|
10
|
15 |
| N.N. |
5
|
x
|
10
|
15 |
| N.N. |
x
|
x
|
10
|
10 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
Elmo muss für seine Geschichtshausaufgaben noch 6 Seiten über die französische Revolution lesen. Doch leider interessiert er sich kein bisschen für dieses Thema und kommt deshalb nur sehr langsam im Text voran. Um seinen Nachmittag mit einem kleinen Erfolgserlebnis aufzuheitern, beschließt er, statt den Text zu lesen, zu zählen, wie viele Vokale und Konsonanten darin vorkommen. Das ist zwar völlig sinnlos, aber immer noch besser als Geschichte!
Nach zwei analysierten Absätzen merkt Elmo, dass diese ganze Zählerei per Hand ziemlich fehleranfällig ist. Kannst du ein Programm schreiben, dass sich nicht verzählt?
Dank deines Programms weiß Elmo jetzt in Sekundenschnelle, wie viele Vokale und Konsonanten der Text besitzt. Doch die gewonnene Zeit will er auf keinen Fall in das Fortführen seiner Hausaufgabe investieren. Daher entscheidet er sich, wahllos Begriffe aus seinem Geschichtsbuch herauszupicken und zu zählen, wie oft sie in der Textpassage, die er noch lesen muss vorkommen, um festzustellen, wie relevant sie für seine Hausaufgabe sind und ob er sie beherrschen sollte.
Kannst du dein Programm vielleicht so erweitern, dass es Elmo auch diese Aufgabe abnimmt und er bevor er müde ist und ins Bett muss noch seine Hausaufgabe fertig machen kann?
Der erste Teil der Eingabedatei buchstaben.in ist der zu analysierende Text. Er besteht ausschließlich aus Kleinbuchstaben von a–z. Leerzeichen, Zahlen, Umlaute oder ähnliches sind nicht enthalten. Die Buchstaben stehen zeilenweise in der Datei, wobei eine Zeile nie länger als 1000 Zeichen ist. Der gesamte Text besteht aus nicht mehr als 1.000.000 Zeichen. Eine leere Zeile signalisiert das Ende des Textes und den Beginn des zweiten Teils der Datei.
Der zweite Teil der Eingabedatei besteht aus 1 ≤ m ≤ 2000 Zeilen. In jeder Zeile befindet sich ein Wort, bestehend aus maximal 100 Kleinbuchstaben von a–z.
Anmerkung: Solltest du dich dazu entscheiden, nur Aufgabenteil 1 zu bearbeiten, besteht keine Notwendigkeit, über die Leerzeile nach dem ersten Teil der Eingabedatei hinaus einzulesen.
In der ersten Zeile der Ausgabedatei buchstaben.out sollen exakt zwei Ganzzahlen getrennt mit einem Leerzeichen stehen. Die erste soll die Anzahl der Vokale im Text, die zweite die Anzahl der Konsonanten angeben.
In den folgenden m Zeilen der Ausgabedatei soll jeweils genau eine Ganzzahl stehen, die die Anzahl der Vorkommnisse des m-ten Wortes des zweiten Teils der Eingabedatei im zu analysierenden Text angibt.
Anmerkung: Solltest du dich dazu entscheiden, nur Aufgabenteil 1 zu bearbeiten, genügt es, nur die erste Zeile der Ausgabedatei auszugeben. Sollte die beiden Zahlen der ersten Zeile richtig und damit Aufgabenteil 1 korrekt gelöst sein, bekommst du 5 Punkte für diesen Testfall. Sollte auch der Rest der Ausgabe korrekt sein, bekommst du 10 Punkte.
Memory: 32 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
| buchstaben.in | buchstaben.out |
| abcacbabcacba abc ab b | 5 8 2 2 4 |
Bei dieser Aufgabe ging es in erster Linie darum, sich an das System zu gewöhnen, das heißt mit dem Einsenden von Programmen und dem Einlesen sowie der Ausgabe von Dateien klarzukommen.
Die Eingabebeschränkungen waren für das Zeitlimit bewußt zu groß gewählt, so daß der Aufgabenteil 2 für Eingabedateien, die die Beschränkungen ausreizen, nicht innerhalb der Zeit lösbar war. Mit dem in der Newsbox gegebenen Hinweis, flush() geschickt zu verwenden, waren aber trotzdem 100 Punkte erreichbar, auch ohne trickreiche Suchalgorithmen zu verwenden oder sein Programm auf die Cache-Größen des verwendeten Prozessors hin zu optimieren.
Im folgenden stellen wir zunächst den Ansatz vor, den wir als Lösung erwartet haben. Danach zeigen wir Alternativen auf, wie man die Laufzeit noch verbessern kann; dies war jedoch nicht verlangt: Beide Ansätze bekamen mindestens 100 Punkte.
Im ersten Aufgabenteil war das zählen von Vokalen und Konsonanten gefordert. Dies macht man am geschicktesten so: In einem Array mit zwei Elementen zählt man im Index 0 die Vokale und im Index 1 die Konsonanten. (Das könnte man auch umgekehrt machen, das ist egal.) Man beginnt in beiden mit Null.
int cnt[2] = {0,0};
Nun untersucht man die Eingabe Zeichen für Zeichen und erhöht das entsprechende Element. Welches Element "entsprechend" ist, hängt nun vom Eingabezeichen ab: Die Zeichen a-z entsprechen den ASCII-Codes 97-122. Ob ein Zeichen nun ein Konsonant oder ein Vokal ist, speichert man in einem konstanten Array:
int tp[] = {0,1,1,1,0,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1,1};
Hat man nun den Text, den ersten Teil der Eingabedatei, in ein Puffer (char buf[1000001];) eingelesen (ohne die Zeilenumbrüche natürlich), so wird die Zähl-Schleife für den Aufgabenteil 1 somit einfach zu:
for(int i = 0; i < length; i++) cnt[tp[buf[i]-'a']]++;
Das 'a' wird hierbei vom Compiler automatisch in 97 umgewandelt.
Sei die Länge des Textes N, so ist die benötigte Zeit für Aufgabenteil 1 linear: O(N).
In Aufgabenteil 2 soll man nun für jedes Wort aus dem zweiten Teil der Eingabedatei die Häufigkeit ausgeben, mit der es im Eingabetext vorkommt.
kommt bald...
Elmo hat einen neuen Job bekommen: Ab sofort ist er Theaterdirektor. Es ist völlig klar, dass ein Theater, das Elmo als Direktor einstellt, kein gewöhnliches Theater sein kann. Und tatsächlich: Es ist eine Mischung aus griechischem Amphitheater und moderner Kunst. In der Mitte befindet sich eine Bühne, drumherum sitzen die Zuschauer. Jedoch sind die Zuschauerreihen nicht in konzentrischen Kreisen, sondern spiralförmig als eine lange Reihe um die Bühne angeordnet.
Elmo denkt sich: Zu einem seltsamen Theater gehört auch eine seltsame Sitzordnung. Er möchte, dass Frauen stets zwischen zwei Männern und Männer stets zwischen zwei Frauen sitzen müssen. Dieses Vorhaben gestaltet sich jedoch als nicht all zu einfach, da in Elmos Theater keine festen Sitzplätze vergeben werden. Es gibt lediglich verschiedene Preiskategorien. Sitze der teuersten Preiskategorie sind beispielsweise die ersten x Sitze (vom inneren Anfang der Sitzspirale aus gezählt).
Die folgende Abbildung zeigt die schematische Darstellung eines Theatersaals, der in insgesamt drei Preiskategorien eingeteilt ist. Zur Preiskategorie 1 gehören die zwölf in rot eingezeichneten Sitze, zur Preiskategorie 2 die 17 in blau eingezeichneten und zur Preiskategorie 3 die elf in grün eingezeichneten.
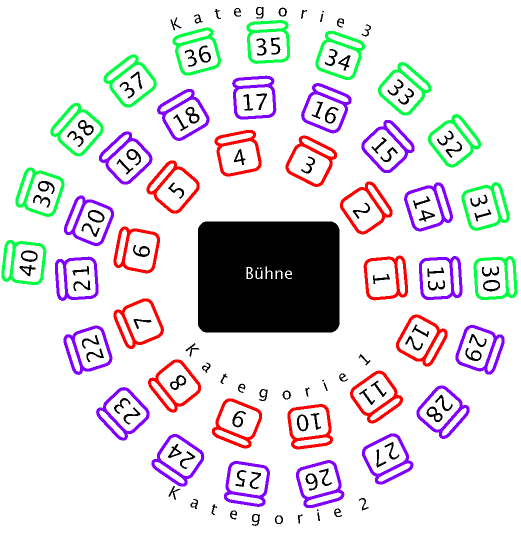
Um festzustellen, wie sehr die von ihm gewünschte Sitzordnung missachtet wird, stellt Elmo sich am Tag der Aufführung an den Eingang und reißt höchstpersönlich die Tickets ab, wobei er sich merkt, wann welches Geschlecht mit einer Eintrittskarte welcher Preiskategorie das Theater betritt. Natürlich weiß Elmo, ab welchem Sitzplatz in seinem Theater welche Preiskategorie beginnt und er weiß auch, dass seine Gäste immer den in der Sitz-Spirale innenliegendsten Platz einnehmen, der noch frei ist und ihrer Preiskategorie entspricht.
Kannst du Elmo mithilfe dieser Informationen helfen, herauszufinden, wie oft seine Sitzordnung missachtet wurde? Als eine Missachtung der Sitzordnung zählt dabei jedes paar zweier gleichgeschlechtlicher Personen, die nebeneinander sitzen. Beachte dabei, dass der letzte Stuhl einer jeden Kategorie direkt an den ersten Stuhl der darauffolgenden Kategorie grenzt. (Der erste Stuhl der ersten und der letzte Stuhl der letzten Kategorie haben natürlich nur einen Nachbarstuhl.)
In der ersten Zeile der Eingabedatei theater.in stehen genau zwei ganze Zahlen, die Anzahl m der Preiskategorien (1 ≤ m ≤ 100) und die Anzahl n der erwarteten Gäste (1 ≤ n ≤ 1.000.000).
In folgenden m Zeilen steht jeweils genau eine ganze Zahl, wobei die i-te dieser Zahlen die Anzahl der Sitzplätze in Kategorie i angibt. Es ist garantiert, dass die Summe dieser m Zahlen genau n ergibt.
In den darauf folgenden n Zeilen steht jeweils ein Buchstabe, gefolgt von einem Leerzeichen und einer ganzen Zahl 1 ≤ k ≤ m. Der Buchstaben sind immer entweder „w“ oder „m“. Dabei gibt der j-te dieser Buchstaben das Geschlecht der j-ten Person und die danebenstehende j-te Zahl die Preiskategorie, die sich diese Person geleistet hat, an.
Deine Ausgabedatei theater.out soll exakt eine Zeile mit einer einzigen ganzen Zahl enthalten: Die Anzahl der Personenpaare, die nebeneinander sitzen und dabei das gleiche Geschlecht haben.
Memory: 32 MB
Laufzeit: 1,5 Sekunden
Programmiersprachen: C, C++, Pascal
| theater.in | theater.out |
| 3 40 12 17 11 m 1 w 3 m 3 m 2 w 2 m 3 w 3 w 1 m 3 w 1 w 3 w 1 w 3 m 1 w 1 m 1 w 1 m 3 m 1 w 1 m 2 w 3 m 3 w 3 m 1 m 1 w 2 m 2 w 2 m 2 w 2 m 2 w 2 m 2 w 2 m 2 w 2 m 2 w 2 m 2 | 6 |
Dieses Beispiel bezieht sich auf die obige Abbildung.
Der erste Gast ist männlich und besitzt eine Preiskategorie 1 Karte. Daher setzt er sich auf Platz 1.
Der zweite Gast ist weiblich und besitzt eine Preiskategorie 3 Karte. Daher setzt sie sich auf Platz 30.
Der dritte Gast ist männlich und besitzt eine Preiskategorie 3 Karte. Der erste Platz in Preiskategorie 3 ist Platz 30, der allerdings schon besetzt ist. Daher setzt er sich uaf Platz 31.
Der vierte Gast ist männlich und besitzt eine Preiskategorie 2 Karte. Daher setzt er sich auf Platz 13.
Der fünfte Gast ist weiblich und besitzt eine Preiskategorie 2 Karte. Platz 13 in Preiskategorie 2 ist schon besetzt. Daher setzt sie sich auf Platz 14.
Und so weiter.
Die resultierende Sitzordnung ist in folgender Abbildung dargestellt:
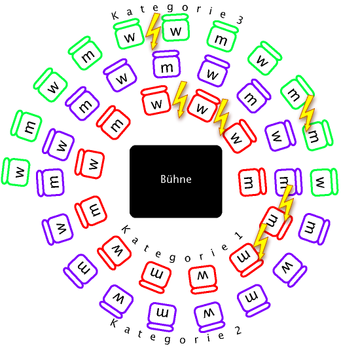
Elmos Sitzregel wurde an sechs Stellen verletzt:
Zwischen Platz 2 und 3, Platz 3 und 4, Platz 11 und 12, Platz 31 und 32, sowie Platz 35 und 36.
kommt bald...
Elmo will sich ein Netz von Handymasten zulegen. Du sollst ihm dabei helfen herauszufinden, welche Gruppe von Masten sich rentieren würde. Die Masten sind nun in einem regelmäßigen Muster verteilt (die schwarzen Punkte in der Grafik). Die Koordinaten der Masten sind dabei in Kilometern angegeben. Die Masten haben in x-Richtung einen Abstand von genau vier Kilometern. Für gerade y Werte steht ein Mast bei x=0 km, für ungerade y Werte steht ein Mast bei x=2 km. Dieses Gitter erstreckt sich in der Ebene unendlich weit.
Gegeben sind nun die Positionen der Handies (beispielsweise die roten Punkte in der Grafik). Jedes Handy wird vom nächstgelegenen Masten versorgt. Die Anzahl der Handys, die ein Mast versorgt, nennt man seine Auslastungzahl.
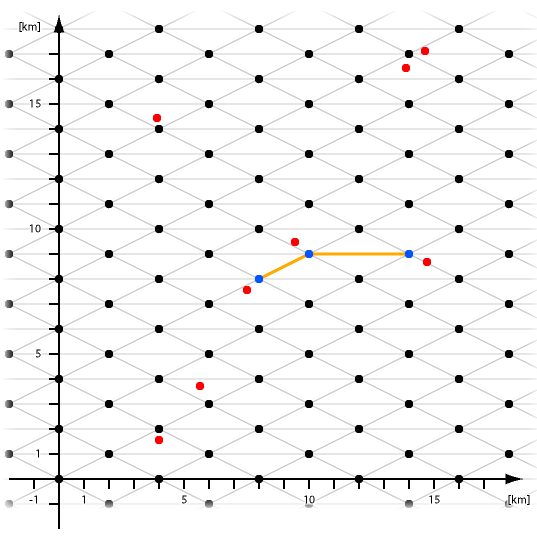
Für jede auftretende Auslastungszahl (außer der Null) sollst du genau die Anzahl der Handymasten angeben, die diese Auslastungzahl besitzen.
Die Masten sind nun durch direkte Kabel verbunden (siehe Grafik). Elmo sucht nun eine Gruppe von Masten, die allesamt eine Auslastungzahl größer als Null haben und die durch Kabel miteinander verbunden sind. (Kabelverbindungen, die über unbeteiligte Masten laufen, gelten hierbei nicht!) Hilf ihm, die größte solche Gruppe zu finden.
In der Eingabedatei handy.in sind die Koordinaten der Handies in Metern angegeben. In der ersten Zeile steht die Anzahl der folgenden Handy-Koordinaten. Danach enthält jede Zeile die x- und y-Koordinate eines Handies, angegeben durch zwei leerzeichen-separierte, ganze Zahlen.
Insgesamt enthält die Datei Beschreibungen zu maximal 50000 Handies. Zu jedem Handy gibt es einen eindeutigen Versorgungsmasten.
Die Koordinaten liegen bis zu im Bereich von -32.000.000 bis 32.000.000.
Der erste Teil der Ausgabedatei handy.out entält je Zeile jeweils eine Auslastungszahl und die zugehörige Anzahl von Handymasten. Die Reihenfolge dieser Zeilen ist egal.
Der zweite Teil der Datei besteht lediglich aus einer Zeile, die nur eine Zahl enthält: Die Anzahl der Masten in der größten Gruppe, die Elmos Wünsche erfüllt.
Memory: 32 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
| handy.in | handy.out |
| 8 3900 14400 4000 1600 5750 3750 7600 7600 9750 9530 13800 16400 14600 8860 14600 17100 | 1 6 2 1 3 |
Es gibt 6 Masten mit der Auslastungszahl 1 und 1 Mast mit der Auslastungszahl 2.
Die größte Gruppe, die die Kriterien erfüllt (siehe Grafik), besteht aus 3 Masten.
kommt bald...
Für seine Mathehausaufgaben muss Elmo lange reihen von Multiplikationen ausführen. Zum Beispiel: 1 ∙ 2 ∙ 3 ∙ 4. Da Elmo von diesen Aufgaben ein wenig unterfordert ist, schweifen seine Gedanken ab. Er überlegt sich: Für das Endergebnis des gesamten Produkts spielt es keine Rolle, welche Multiplikation zuerst ausgerechnet wird. Um zu verdeutlichen, in welcher Reihenfolge man die Multiplikationen ausgerechnet hat, kann man jedoch Klammern setzen. Zum Beispiel so: ((1 ∙ 2) ∙ (3 ∙ 4)). Hier hat Elmo zuerst (1 ∙ 2), dann (3 ∙ 4) und schließlich (2 ∙ 12) ausgerechnet. Das führt Elmo zu der Frage: Wie viele Möglichkeiten gibt es insgesamt, einen solchen Ausdruck zu klammern? Kannst du ihm diese Frage beantworten?
Etwas formaler formuliert: Wieviele Möglichkeiten gibt es, den Ausdruck a1a2a3…an zu klammern, so dass
Beispielsweise gibe es genau 5 Möglichkeiten, a1a2a3a4 zu klammern:
Die Eingabedatei klammerwald.in besteht aus einer einzigen Zeile mit einer einzigen Ganzzahl, n mit 1 ≤ n ≤ 250, die die Anzahl der ai im Ausdruck angibt.
Die Ausgabedatei klammerwald.out soll aus einer einzigen Zeile mit einer einzigen Ganzzahl bestehen, die die Anzahl der verschiedenen Klammerungen für den spezifizierten Ausdruck angibt. Beachte, dabei, dass diese Zahl mit wachsendem n sehr schnell ziemlich groß wird.
Der C/C++ Typ „long long“, sowie der Pascal Typ „Int64“ sind 64 Bit Integer.
In C++ und Pascal werden diese Typen genau so ein- und ausgelesen wie 32 Bit Integer Typen. In C kann man sie mit scanf, printf, etc. mit der Konvertierung „%lld“ ein- bzw. ausgeben.
Memory: 32 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
| klammerwald.in | klammerwald.out |
| 4 | 5 |
Für einen Ausdruck der Länge 4 gibt es 5 verschiedene Möglichkeiten, ihn wie angegeben zu klammern.
kommt bald...