 .
.Dies sind die Ergebnisse des 6. OWINF vom 06.12.2008. Wir gratulieren allen Teilnehmern ganz herzlich zu Ihrem Erfolg.
| Name | gelaende | ottcode | wettbewerb | ∑ |
|---|---|---|---|---|
| Fabian Gundlach |
100
|
70
|
65
|
235 |
| Markus König |
100
|
20
|
65
|
185 |
| Oleg Yuschuk |
95
|
20
|
65
|
180 |
| Nikolai Wyderka |
95
|
50
|
25
|
170 |
| Paul Görlach |
95
|
0
|
65
|
160 |
| Eike Müller |
95
|
40
|
20
|
155 |
| Jochen Eisinger |
35
|
10
|
95
|
140 |
| Oliver Siebert |
95
|
10
|
30
|
135 |
| Robert Czechowski |
95
|
10
|
30
|
135 |
| Aaron Montag |
55
|
10
|
65
|
130 |
| Max Haslbeck |
85
|
10
|
30
|
125 |
| Alexej Chemissov |
90
|
0
|
30
|
120 |
| Thi Bui-Ngoc |
95
|
0
|
25
|
120 |
| Simon Blessenohl |
95
|
x
|
20
|
115 |
| N.N. |
95
|
x
|
10
|
105 |
| N.N. |
95
|
x
|
x
|
95 |
| Fabian Beckmann |
10
|
50
|
25
|
85 |
| Stephan Gocht |
x
|
x
|
75
|
75 |
| Erwin Goslawski |
30
|
0
|
20
|
50 |
| N.N. |
40
|
x
|
5
|
45 |
| N.N. |
25
|
0
|
20
|
45 |
| N.N. |
15
|
x
|
30
|
45 |
| N.N. |
20
|
0
|
20
|
40 |
| N.N. |
x
|
10
|
30
|
40 |
| N.N. |
10
|
x
|
15
|
25 |
| N.N. |
x
|
x
|
20
|
20 |
| N.N. |
x
|
x
|
20
|
20 |
| N.N. |
x
|
0
|
20
|
20 |
| N.N. |
x
|
x
|
20
|
20 |
| N.N. |
20
|
0
|
0
|
20 |
| N.N. |
x
|
x
|
20
|
20 |
| N.N. |
x
|
x
|
15
|
15 |
| N.N. |
x
|
0
|
15
|
15 |
| N.N. |
x
|
x
|
10
|
10 |
| N.N. |
x
|
x
|
10
|
10 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
0
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
0
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
x
|
x
|
0 |
| N.N. |
x
|
0
|
0
|
0 |
Elmo möchte auf seinem Computer eine Berechnung durchführen, die D Stunden dauert und die er zu einer vollen Stunde starten wird. Leider ist sein Computer aber instabil, so daß er gelegentlich abstürzt. Da Elmo dann jedesmal per Hand das Programm, das die Berechnung dann weiter durchführt, wieder starten muß, würde er gerne im Voraus ungefähr wissen, wie wahrscheinlich es ist, daß sein Computer in den D Stunden mindestens einmal abstürzt. Außerdem will er wissen, wie wahrscheinlich es ist, daß er in dem Zeitraum mindestens zweimal, mindestens dreimal, usw. abstürzt.
Um dies abschätzen zu können, hat er ein Protokoll geführt, wann sein Computer in der Vergangenheit abgestürzt ist. Sein Protokoll beginnt zur (vollen) Stunde S und endet zur (vollen) Stunde E (gezählt seit dem Jahreswechsel 1969/1970). Jedesmal, wenn sein Computer abgestürzt ist, hat ein Skript von Elmo die aktuelle Stunde ins Protokoll geschrieben. Sein Computer war in der Zeit von S bis E durchweg angeschaltet.
Hilf Elmo abzuschätzen, wie häufig er sein Berechnungsprogramm neu starten muß.
In der ersten Zeile der Eingabedatei absturz.in stehen die Zahlen D, S, E und N. Dabei ist N die Anzahl der Einträge im Absturzprotokoll.
Die nächsten N Zeilen enthalten die Einträge des Protokolls, aufsteigend sortiert.
In der k-ten Zeile der Ausgabedatei absturz.out soll die Wahrscheinlichkeit stehen, dass der Computer in den D Stunden der Berechnung mindestens k-mal abstürzt. Dabei sollst Du einen Bruch zweier natürlicher Zahlen verwenden, um Rundungsfehler auszuschließen. Der Bruch muß nicht gekürzt ein.
Das Ende dieser Folge (das aus lauter Nullen besteht) soll nicht ausgegeben werden.
Memory: 16 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
0≤S<E≤2 000 000 000
0<D≤E-S
D≤100 000
0≤N≤1 000 000
| absturz.in | absturz.out |
| 10 1000 1109 3 1012 1050 1052 | 11/50 2/25 |
Das Protokoll umfaßt 109 volle Stunden. Nach der Schätzung ist die Wahrscheinlichkeit, dass die 10-Stunden-Berechnung mindestens einmal abstürzt 11/50, dass sie zweimal abstürzt 2/25 und dass sie dreimal oder mehrfach abstürzt 0.
Das Problem ist ein typisches scanline-Problem (auch wenn es mit dem Wikipedia-Artikel "Scanline-Algorithmus" nur bedingt zu tun hat):
Wenn man alle möglichen Kombinationen, die ein D breites Fenster auf dem Intervall [S,E] bei ganzzahligen Randkoordinaten haben kann, durchprobiert, testet man E-S-D+1 Möglichkeiten durch:
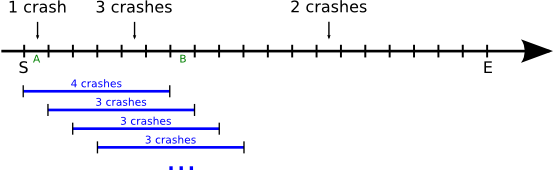
Selbst wenn man in jedem Schritt die Anzahl der Abstürze effizient berechnet, d.h. die Anzahl im neuen Fenster aus der im alten berechnet (plus die in der nächsten Stunde minus die in der letzten Stunde: "-A+B" im ersten Schritt, so braucht man immer noch E-S-D+1, also maximal 2 000 000 000, Iterationen, was zu viel ist.
Der Trick ist, zu erkennen, daß N nur relativ klein sein kann. Das heißt, daß bei den meisten Fensterschritten nichts passieren wird. Diese Schritte kann man dann zusammenfassen, d.h. das Fenster gleich um mehrere Positionen weiterschieben:

Wie weit man jeweils weiterschieben darf, hängt davon ab, wann der nächste crash links
das Fenster verläßt und wann der nächste crash rechts ins Fenster eintritt (oder wann das Fenster rechts E
erreicht).
Dazu hält das Programm die Indizes left und right in das crash-Array, die angeben, welcher
Crash als nächstes die linke bzw. rechte Fenstergröße passieren wird. step ist die Anzahl der nächsten
Schritte, in denen nichts interessantes passiert und die also übersprungen werden können. current ist
die Anzahl der crashes im aktuellen Fenster.
In count[x] wird dann die Anzahl berechnet, wie häufig x Abstürze in dem Fenster der Breite D vorkamen.
Am Ende über alle jeweils größeren Indizes aufsummiert ergibt dieses Array die Ausgabedatei.
Zu Beginn wird an das crash-Array noch ein "Pseudo-Crash" bei E+D+2 angehängt, über den das Fenster nie hinwegkommen wird (das stoppt ja bei E), damit nicht extra überprüft werden muß, ob left oder right das Ende des Arrays erreicht haben.
Da das Fenster für jeden Absturz maximal zweimal anhält (rechts und links), also 2*N Mal, hat das Programm eine Laufzeit von O(N), was akzeptabel ist.
#include <cstdio>
#include <queue>
using namespace std;
int main() {
freopen("absturz.in","r",stdin);
freopen("absturz.out","w",stdout);
int D, S, E, N;
scanf("%d %d %d %d", &D, &S, &E, &N);
E -= S;
int P[1000001];
for (int n = 0; n < N; n++) {
scanf("%d", &P[n]);
P[n] -= S - 1;
}
P[N] = E + D + 2;
int count[N];
for (int c = 0; c < N; c++)
count[c] = 0;
int max_crashes = 0;
int left = 0;
int right = 0;
int last = 0;
while (P[right] <= D) right++;
int current = right;
while (last != E - D + 1 ) {
int step = min(min(P[left] - last, P[right] - D - last), E - D + 1 - last);
count[current] += step;
if (current > max_crashes)
max_crashes = current;
last += step;
while (P[left] <= last) {
left++;
current--;
}
while (P[right] <= last + D) {
current++;
right++;
}
}
for (int i = max_crashes - 1; i >= 0; i--) {
count[i] += count[i+1];
}
for (int i = 1; i <= max_crashes; i++) {
printf("%d/%d\n", count[i], E-D+1);
}
return 0;
}
Viele Programmierwettbewerbe funktionieren nach folgendem Prinzip: Es gibt N Aufgaben, die gelöst werden können. Anders als beim OWINF kann eine Aufgabe nur entweder vollständig oder aber gar nicht gelöst werden. Wer die meisten Aufgaben vollständig richtig löst, gewinnt. Wenn allerdings zwei Teilnehmer die gleiche Anzahl an Aufgaben gelöst haben, dann gewinnt der Teilnehmer mit der geringeren Zeitpunktzahl. Die Zeitpunktzahl wird berechnet, indem jedesmal, wenn eine weitere Aufgabe richtig gelöst wird, die Zeit in Minuten, die seit dem Beginn des Wettbewerbs verstrichen ist, zur aktuellen Zeitpunktzahl dazu addiert wird. Zu Beginn des Wettbewerbs ist die Zeitpunktzahl jedes Teilnehmers selbstverständlich 0. Ungelöste Aufgaben tragen nicht zur Zeitpunktzahl bei.
Wenn beispielsweise in einem solchen Wettbewerb mit drei Aufgaben ein Teilnehmer die erste Aufgabe nach 30 Minuten, die zweite Aufgabe nach 45 und die dritte Aufgabe nach 90 Minuten löst, dann ist seine Zeitpunktzahl 30 + 45 + 90 = 165.
Wir gehen davon aus, dass ein Teilnehmer immer nur eine Aufgabe gleichzeitig bearbeitet und (erfolgreich) einschickt, bevor er mit der Bearbeitung der nächsten Aufgabe anfängt. Außerdem gehen wir davon aus, dass die Zeit zum Lösen einer Aufgabe eine ganze Zahl in Minuten ist, d.h. Sekunden, Millisekunden, etc. werden ignoriert. Das bedeutet, dass der Teilnehmer in diesem Beispiel 30 Minuten für die erste Aufgabe, 15 Minuten für die zweite Aufgabe, und 45 Minuten für die dritte Aufgabe braucht. Wenn er zuerst die zweite Aufgabe, danach die erste Aufgabe und dann die dritte Aufgabe gelöst hätte, dann wäre seine Zeitpunktzahl nur 15 + 45 + 90 = 150 gewesen. Es ist in diesem Fall also möglich, eine bessere Zeitpunktzahl zu erzielen, indem man seine Aufgaben in einer anderen Reihenfolge bearbeitet.
Dein Programm soll eine Liste mit den Zeiten (in Minuten) nach Wettbewerbsanfang, zu dem ein bestimmter Teilnehmer seine Aufgaben richtig eingeschickt hat, einlesen. Es soll ausrechnen, wieviele Zeitpunkte der Teilnehmer maximal hätte einsparen können, wenn er die Aufgaben in einer optimalen Reihenfolge bearbeitet hätte.
In der ersten Zeile der Eingabedatei wettbewerb.in steht eine ganze positive Zahl N, die Anzahl der Aufgaben im Wettbewerb.
Die nächsten N Zeilen enthalten die Zeitpunkte, zu denen die einzelnen Aufgaben richtig gelöst wurden: Zeile 1 + i beinhaltet ti, die Anzahl der Minuten nach Beginn des Wettbewerbs bis zum Zeitpunkt, zu dem die Aufgabe erfolgreich eingeschickt wurde. Wenn die Aufgabe bis zum Ende des Wettbewerbs nicht gelöst wurde, dann ist ti = -1.
Eine ganze natürliche Zahl: Die maximale Anzahl der Zeitpunkte, die der Teilnehmer hätte einsparen können, wenn er die Reihenfolge zur Bearbeitung der Aufgaben optimal gewählt hätte.
Memory: 16 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
0 < N ≤ 1 000 000
-1 &le ti ≤ 1 000 000 000 (1 ≤ i ≤ N)
Die Bearbeitung einer Aufgabe dauert mindestens eine Minute.
| wettbewerb.in | wettbewerb.out |
| 3 30 45 90 | 15 |
Es handelt sich bei der Eingabe um das im Text beschriebene Beispiel.
Das schwierigste an dieser Aufgabe ist es, die riesigen Eingabedateien schnell genug in den Speicher zu laden. Dazu wird getline und die C-Funktion atol verwendet. Liest man direkt aus der Datei mit operator>> schafft man es nicht den letzten Testfall rechtzeitig zu lösen...
Die Lösung besteht sonst aus vier Schritten:
Würde man eine kurze Aufgabe (sagen wir der Länge l) vom Anfang um n Minuten nach hinten verschieben, dann würde sie in der Summe mit n+l statt nur mit l Punkten gezählt werden.
Ein anderes Problem, dass viele Einsender hatten, war, dass nicht bedacht wurde, dass die Summe der Zeitpunkte mehr als 32bit braucht. Daher verwendet die Musterlösung den Datentyp int64_t.
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <fstream>
#include <algorithm>
int main() {
std::ifstream inf("wettbewerb.in");
std::ofstream outf("wettbewerb.out");
int N;
char line[32];
inf.getline(line, 32);
N = atol(line);
std::vector<int64_t> duration;
int64_t original_sum = 0, last = 0;
for (int i=0; i<N; ++i) {
int t;
inf.getline(line, 32);
t = atol(line);
if (t > 0) {
duration.push_back(t);
original_sum += t;
}
}
std::sort(duration.begin(), duration.end());
for (int i=0; i<duration.size(); ++i) {
last = duration[i] - last;
std::swap(duration[i],last);
}
std::sort(duration.begin(), duration.end());
int64_t sum=0;
last = 0;
for (int i=0; i<duration.size(); ++i) {
sum += (last + duration[i]);
last += duration[i];
}
outf << original_sum - sum << "\n";
return EXIT_SUCCESS;
}
Elmo hat es wieder gepackt. Vorgestern hat er auf dem Dachboden eine Umzugskiste mit alten Computerspielen gefunden. Seit er herausgefunden hat, daß sein SimCity 2000 von Maxis noch auf seinem PC läuft, hat er seine Wohnung nicht mehr verlassen.
Während er sich gerade auf seinem Schreibtischsessel zurücklehnt, lächelnd die Autokolonnen verfolgt und langsam ins schwärmen über alte Zeiten kommt, hat der algorithmische Teil seines Gehirns schon längst die nächste Aufgabe gefunden: Für eine neue exklusive Wohngegend sucht er ein geeigneten Platz. Dabei soll die Gegend möglichst hoch liegen, und dabei möglichst groß sein. Dabei zählen diagonal liegende Planquadrate nicht als benachbart.
Durch einen glücklichen Zufall hat er herausgefunden, wie er die Höhe jedes Planquadrats aus einem gespeicherten Spielstand auslesen kann. Du sollst ihm nun helfen, die Investitionskosten abzuschätzen, indem Du die Größe des gesuchten Gebietes bestimmst.
In der ersten Zeile der Eingabedatei gelaende.in stehen die ganzen Zahlen B und H, die Breite und Höhe des Spielfeldes.
In der i-ten der nächsten H Zeilen steht in der j-ten der jeweils B Spalten die ganze Zahl hij, die die Höhe des Planquadrats mit den Koordinaten (i,j) beschreibt.
In der Ausgabedatei gelaende.out steht in der einzigen Zeile die Größe der Gegend, die möglichst hoch liegt, und dabei möglichst groß ist.
Laufzeit: 1 Sekunde
Speicher: 16 Megabyte
0<B≤1000
0<H≤1000
0≤hij≤1000 für alle i,j.
| gelaende.in | gelaende.out |
| 9 10 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 3 2 1 1 5 1 1 0 1 3 5 1 0 1 5 1 0 1 0 2 1 0 1 5 1 0 1 1 1 1 0 1 5 1 0 0 0 0 0 0 1 5 1 0 1 1 1 0 0 1 5 1 0 1 3 1 0 0 1 5 1 0 1 1 1 0 0 1 1 1 | 6 |
Die höchste und dabei größte Gegend besteht aus den 5en in der achten Spalte. Die 5 in der siebten Spalte zählt nicht mehr zu der Gegend, da sie nur diagonal angrenzt.
Diese Aufgabe ist relativ einfach, erfordert aber ein bisschen Tipparbeit, da man eine Datenstruktur implementieren muss, die nicht in der STL ist...
Das Programm verwaltet Mengen von Feldern, die jeweils zusammenhängend sind. Da im Laufe der Berechnung solche Mengen vereinigt werden können, werden diese in einer sogenannten union-find Datenstruktur gespeichert (siehe zB Wikipedia). Diese Datenstruktur erlaubt es einem (a) Mengen schnell zu vereinigen und (b) festzustellen, zu welcher Menge ein gegebenes Element gehört.
Nachdem die Geländebeschreibung geladen wurde, geht man alle Felder durch, und schaut ob einer der zwei Vorgänger (linker bzw. oberer Vorgänger) auf den höchsten Niveau sind. Ist dies der Fall, wird das Feld mit der Menge, zu der sein Vorgänger gehört, vereinigt. Hat das Feld zwei Vorgänger, so werden auch diese Mengen vereinigt.
Um am Schluss die maximale Fläche bestimmen zu können, wurde die union-find Datenstruktur so erweitert, dass sie die Größen der Mengen mitführt.
#include <cstdlib>
#include <fstream>
#include <vector>
#include <iostream>
struct union_find {
size_t newset() {
size_t n = nodes.size();
nodes.push_back(std::pair<int,int>(n, 0));
size.push_back(1);
return n;
}
void join(size_t x, size_t y) {
int xroot = find(x);
int yroot = find(y);
std::pair<int,int>& xnode = nodes[x];
std::pair<int,int>& ynode = nodes[y];
if (xnode.second > ynode.second) {
ynode.first = xroot;
size[xroot] += size[yroot];
} else if (xnode.second < ynode.second) {
xnode.first = yroot;
size[yroot] += size[xroot];
} else if (xroot != yroot) {
ynode.first = xroot;
xnode.second++;
size[xroot] += size[yroot];
}
}
size_t find(size_t x) {
if (nodes[x].first == x)
return x;
nodes[x].first = find(nodes[x].first);
return nodes[x].first;
}
std::vector<std::pair<int, int> > nodes;
std::vector<int> size;
};
int main() {
std::ifstream inf("gelaende.in");
std::ofstream outf("gelaende.out");
int B, H;
inf >> B >> H;
std::vector<std::vector<int> > map;
int maximum = -1;
for (int h=0; h<H; ++h) {
map.resize(map.size()+1);
for (int b=0; b<B; ++b) {
int height;
inf >> height;
if (height > maximum)
maximum = height;
map.back().push_back(height);
}
}
union_find uf;
for (int h=0; h<H; ++h)
for (int b=0; b<B; b++) {
if (map[h][b] != maximum) {
map[h][b] = -1;
continue;
}
int candidate = -1;
if ((h > 0) && (map[h-1][b] != -1)) {
candidate = map[h-1][b];
}
if ((b > 0) && (map[h][b-1] != -1)) {
int val = map[h][b] = map[h][b-1];
uf.size[uf.find(val)]++;
if ((candidate == -1) || (candidate == val)) {
continue;
}
uf.join(candidate,val);
continue;
}
if (candidate == -1) {
map[h][b] = uf.newset();
continue;
}
map[h][b] = candidate;
uf.size[uf.find(candidate)]++;
}
maximum = 0;
for (int i=0; i<uf.size.size(); ++i)
if (uf.size[i] > maximum)
maximum = uf.size[i];
outf << maximum << "\n";
return EXIT_SUCCESS;
}
Otto hatte es gewusst. Ihm war klar gewesen, dass dies eines Tages passieren würde und jetzt war es soweit:
Nach einer Woche Schulausflug in Barcelona, wo er abgelenkt durch Gaudi, Strände und die Erfahrung der südländischen Lebensweise gar nicht daran dachte in die Reichweite eines Internetcafes zu gehen, steht er nur braungebrannt und erholt aber schockiert vor seinem Computer. Er hat sein Universalpasswort, das er dummerweise für seinen EMail-Account, seine Benutzeranmeldung und alles andere wichtige benötigt, vergessen.
"So klar, dass das kommen musste". Nicht ohne Grund hatte er sich vor einiger Zeit eine todsichere Methode überlegt, wie er - und nur er - sein Passwort sichern und wiederherstellen kann, ohne dadurch ein Sicherheitsrisiko einzugehen.
Er hatte seinen N Freunden jeweils einen Buchstaben des Codes verraten - jedem genau einen. Dies tat er so, dass man, wenn man jeden Freund seinen Buchstaben auf ein Blatt Papier schreiben ließe, diese durch Umsortieren das Passwort ergaben. Weil er das Passwort besonders sicher haben wollte, benutzter er nicht nur die 26 Kleinbuchstaben a-z des deutschen Alphabetes, sondern auch die Ziffern 0-9.
Da er im Fall der Fälle nicht wahlos probieren wollte, bis er ein Wort kombiniert hat, von dem er glaubt, dass es sein Kennwort sein könne, hat er sich zusätzlich noch eine Zahl Z auf die Hinterseite seinen Monitors geschrieben. Sie gibt an, die wievielte Kombination (beginnend bei 1) aus den gegebenen Buchstaben sein Passwort ist, und zwar nach der Reihenfolge sortiert, in der man die verschiedenen kombinierbaren Worte in einem Wörterbuch finden würde (dabei ist die Ordnung über den verwendeten Zeichen 0 < 1 < ... < 9 < a < ... < z ).
Sind beispielsweise die Buchstaben 'o', 'e', 'n', so lassen sich damit die Worte eno, eon, neo, noe, oen und one (die hier bereits richtig sortiert sind) erzeugen. Zusammen mit Z=4 weiß er, dass noe sein Passwort war.
Hilf Otto nun aus dem Zettel mit den gesammelten Buchstaben der Freunde und der Zahl auf seinem Monitor das Passwort wieder zu finden.
Du kannst davon ausgehen, dass Otto nicht mehr als 100 mindestens aber 2 Freunde hat.
Die Eingabe besteht aus mehreren Testfällen in denen du jeweils für Otto ein Passwort finden sollst. Jeder Testfall besteht aus genau einer Zeile. Diese enthält zunächst die Buchstaben und Zahlen (a-z, 0-9) der Freunde direkt hintereinander geschrieben gefolgt von einem Leerzeichen ' ' und der Zahl Z direkt darauf folgend. Es gibt für einen Satz von Buchstaben jeweils maximal 2^60 mögliche verschiedene kombinierbare Worte. Abgeschlossen wird die Eingabe von einer Zeile mit ausschließlich dem Zeichen '#' enthalten.
| Zeile | Inhalt |
|---|---|
| 1: | oen 4 |
| 2: | w1nfo 92 |
| 3: | # |
Gib für jeden Testfall das gesuchte Passwort von Otto in einer eigenen Zeile aus.
| Zeile | Inhalt |
|---|---|
| 1: | noe |
| 2: | ow1nf |
Memory: 16 MB
Laufzeit: 1 Sekunde
Programmiersprachen: C, C++, Pascal
Die Aufgabe ist es, eine die Z-te eindeutige Permutation der Buchstaben zu berechnen, d.h. doppelte Permutationen werden nicht mitgezählt. Trotzdem wird hier zunächst ein Algorithmus erklärt, der doppelte Permutation mitzählt. Dieser wird dann im zweiten Schritt modifiziert, so dass Duplikate nicht berücksichtigt werden.
Angenommen, die Buchstaben des Passworts sind a, b, c und d. Dann gibt es 4! = 24 verschiedene Permutationen:
a b c d // 1. Permutation a b d c a c b d a c d b a d b c a d c b b a c d // 7. Permutation b a d c b c a d b c d a b d a c b d c a c a b d // 13. Permutation c a d b c b a d c b d a c d a b c d b a d a b c // 19. Permutation d a c b d b a c d b c a d c a b d c b a
Man sieht recht schön, dass alle 6 (= 3!) Schritte der erste Buchstabe wechselt. Legt man den ersten Buchstaben fest, so wechselt der zweite alle 2 (= 2!) Schritte, usw... Damit kann man dann leicht ausrechnen, welcher Buchstabe an welcher Position kommt: Sucht man zB die 10. Permutation, so ist der erste Buchstabe b, da alle Permutationen, die mit b anfangen, zwischen 7 und 12 liegen.
Folgender Pseudocode berechnet die Z-te Permutation
int n = chars.size();
int f = factorial(n-1);
for (int i=0; i<chars.size(); ++i) {
int pos = ((Z - 1) / f);
Z -= pos * f;
for (int j=i+pos; j>i; --j) {
std::swap(chars[j],chars[j-1]);
}
f /= (n-1-i);
}
chars ist dabei ein Vektor, in dem die Buchstaben (sortiert) stehen. Die Funktion factorial(n) berechnet den Wert n!. Bereits für kleine n passt n! nicht mehr in einen int, aber das soll uns hier nicht weiter stoören. Die Schleife geht also alle Positionen durch und berechnet, welcher Buchstabe an diese Position soll. In unserem Beispiel mit abcd und Z = 10 würde also der Buchstabe b an die erste Position kommen. Da somit die ersten 6 Permutation übersprungen wurden, wird Z auf 4 angepasst. Der Buchstabe b wird nach vorne verschoben und f wird von (n-1)! auf (n-2)! angepasst.
Mit dieser Lösung wird man leider nur 10 Punkte erreichen, da in der Aufgabenstellung gefordert wird, dass nur eindeutige Permutationen gezählt werden. Dies kann man durch wenige Modifikationen des Algorithmus erreichen.
Sind zum Beispiel die Buchstaben a, b und b gegeben, dann gibt es 3 eindeutige Permutationen:
a b b // 1. Permutation b a b // 2. Permutation b b a
In diesem Fall sind die Blöcke nicht mehr gleichgroß. Deshalb kann man nicht einfach durch eine ganzzahlige Division den Buchstaben berechnen, der als nächstes kommt. Stattdessen muss man für jeden möglichen Buchstaben ausrechnen, wieviele mögliche Kombinationen es gibt.
Die Anzahl der möglichen eindeutigen Permutationen kann man mit dem sogenannten Polynomialkoeffizient bestimmen (siehe zB Wikipedia). Dabei ist n die Anzahl der Buchstaben und ri die Häfigkeit des i-ten Buchstabens.
Zurück zu unserem Beispiel. Für a gibt es 2!/(0!2!) = 1 Möglichkeiten die anderen Buchstaben anzuordnen. Für b gibt es 2!/(1!1!) = 2 Möglichkeiten.
Bleibt nur noch das Problem, den Polynomialkoeffizient auszurechnen. Dies kann einfach auf den Binomialkoeffizient zurückgeführt werden mit
n!/(r1! r2! ... rm!) = n!/(r1!(n-r1)!) * (n-r1)!/(r2! ... rm!)
Damit haben wir alle Sachen zusammen, um die Aufgabe zu lösen.
#include <cstdlib>
#include <fstream>
#include <vector>
#include <algorithm>
#include <string>
#include <iostream>
#include <map>
uint64_t binom(uint64_t n, uint64_t m) {
std::vector<uint64_t> b(n+1);
b[0] = 1;
for (uint64_t i=1; i<=n; ++i) {
b[i] = 1;
for (uint64_t j= i-1; j>0; --j)
b[j] += b[j-1];
}
return b[m];
}
uint64_t multinom(uint64_t n, std::vector<uint64_t>& m) {
std::sort(m.begin(), m.end(), std::greater<uint64_t>());
uint64_t result = 1;
for (int i=0; i<m.size(); ++i) {
result *= binom(n,m[i]);
n -= m[i];
}
return result;
}
int main() {
std::ifstream inf("ottcode.in");
std::ofstream outf("ottcode.out");
for (;;) {
std::string letters;
uint64_t Z;
std::vector<char> chars;
std::map<char,int> count;
inf >> letters;
if (letters == "#")
break;
inf >> Z;
Z--;
for (int i=0; i<letters.size(); ++i) {
count[(size_t)letters[i]]++;
chars.push_back(letters[i]);
}
std::vector<uint64_t> m;
for (std::map<char,int>::const_iterator i = count.begin();
i != count.end(); ++i)
m.push_back(i->second);
uint64_t factorial = multinom(chars.size(), m);
std::sort(chars.begin(), chars.end());
uint64_t n = chars.size();
for (uint64_t i=0; i<chars.size()-1; ++i) {
uint64_t perm = 0;
int pos = 0;
std::map<char,int>::iterator c = count.begin();
for (;;) {
if (c->second > 0) {
uint64_t cmb = factorial * (uint64_t)c->second / (n-i);
perm += cmb;
if (perm > Z) {
Z -= (perm - cmb);
factorial = cmb;
c->second--;
break;
}
}
pos+=c->second;
c++;
}
for (int j = i+pos; j>i; --j)
std::swap(chars[j], chars[j-1]);
}
for (int i=0; i<chars.size(); ++i)
outf << chars[i];
outf << "\n";
}
return EXIT_SUCCESS;
}
In der Funktion binom wird der Binomialkoeffizient berechnet. Damit kann dann die Funktion multinom den Polynomialkoeffizient (engl. multinomial) berechnen. Der Rest ist im wesentlichen so, wie im einfacheren Fall, nur dass für jeden Buchstaben berechnet werden muss, wieviele Permutationen möglich sind, und entsprechend mitgezählt werden muss, wieviele Buchstaben noch zur Verfügung stehen (in der map count).